Introduction
The
function provided here can be used to
draw a text string
with an oblique or
slant angle. Such
text
outputs are useful in isometric or
perspective 3D views to make the
text strings
look like in their 3D space. An example is
shown in the following picture:

Background
Windows GDI
function
TextOut()
does not allow a
text slant angle. To
draw
such slanted
strings, we need to set a
transformation using
SetWorldTransform().
Windows drawing
function will then take care of the shearing
and rotation of the output. This procedure
is incorporated into a new function similar
to Windows
TextOut()
function:
void ObliqueTextOut( CDC *dc, int oblique, int x,int y,const CString &Text )
This
function has the same arguments as Windows
TextOut()
function with an additional argument,
oblique,
to specify the text
slant angle. The function can be
placed where
TextOut()
is normally used.
Using
the code
Insert
the function source
code into your
source code
file. Call the function at places where you
would normally call Windows
TextOut()
function. Remember to select the font, set
the text background mode, color and
background color etc, as you would normally
do before calling
TextOut().
Angle
oblique
is positive if the
text slants forward(to the right)
and negative if it
slants backwards(to the left).
The
oblique
angle,
s,
in the figure below is positive. The angle
is in 1/10th degrees. Therefore, if the
text slants forward 15 degrees,
oblique=150.
Points of Interest
The
key to the question is to set up the
transformation in DC. Function
SetWorldTransform()
needs an
XFORM
structure for the transformation. Therefore,
we need to prepare the
XFORM
structure before calling
SetWorldTransform(
).
XFORM
has 6 member data. They are
eM11,
eM21,
eM12,
eM22,
eDx,
eDx.
They are defined as:
X = eM11 * x + eM21 * y + eDx
Y = eM12 * x + 2M22 * y + eDy
where
(x,y)
are the
World coordinates and
(X,Y)
are the Paper space coordinates.
In the
figure below,
x,y
are the World space axes. The string will
always be drawing at
(0,0)
and horizontally in the world space.
xs,ys
are the
Sheared space axes. The transformation from
World to the Sheared space is:
xs = x - y * tan(s)
ys = y
where
s
is the slant
or oblique angle.
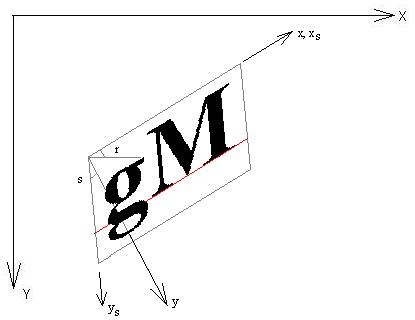
The
Paper space is noted as
X,Y.
From the Sheared space to Paper space, the
transformation is a
rotation(angle
r)
and translation(Xo,Yo).
X = Xo + xs * cos(r) + ys * sin(r)
Y = Yo + ys * cos(r) - xs * sin(r)
Where
(Xo,Yo)
are simply the text insertion point in Paper
space. Substitute
(xs,ys)
into the above, we get:
X = cos(r) * x + (sin(r)-tan(s)*cos(r)) * y + Xo
Y = -sin(r) * x + (cos(r)+tan(s)*sin(r)) * y + Yo
Compare this to the
XFORM
structure, it is obvious that:
eM11 = cos(r)
eM21 = sin(r) - tan(s) * cos(r)
eM12 = -sin(r)
eM22 = cos(r) + tan(s) * sin(r)
eDx = Xo
eDy = Yo
The
above is translated into function code(dc
is the
input device context):
XFORM xForm;
xForm.eDx = (float) x;
xForm.eDy = (float) y;
xForm.eM11 = (float) cos(txtRotate);
xForm.eM21 = (float) (sin(txtRotate) - tan(txtOblique)*cos(txtRotate));
xForm.eM12 = (float) -sin(txtRotate);
xForm.eM22 = (float) (cos(txtRotate) + tan(txtOblique)*sin(txtRotate));
SetGraphicsMode( dc->m_hDC, GM_ADVANCED );
SetWorldTransform( dc->m_hDC, &xForm );
The
call to
SetGraphicsMode()
is
needed. Otherwise, function
SetWorldTranform()
will
have no effect. Since now we are drawing in
World space, we need to adjust the font's
rotation(lfEscapement)
to be horizontal and the character
orientation(lfOrintation)
to be from the World X-axis.
LOGFONT lgf;
dc->GetCurrentFont()->GetLogFont( &lgf );
...
lgf.lfOrientation -= lgf.lfEscapement;
lgf.lfEscapement = 0;
CFont horFont;
horFont.CreateFontIndirect( &lgf );
CFont *OldFont = dc->SelectObject( &horFont );
Now,
we can call:
dc->TextOut( 0,0, Text );
The
work is done. But before returning, we need
to restore the graphics mode and font:
ModifyWorldTransform( dc->m_hDC, &xForm, MWT_IDENTITY );
SetGraphicsMode( dc->m_hDC, GM_COMPATIBLE );
dc->SelectObject( OldFont );





